Una vez recogidos los datos, mediante encuestas por ejemplo, se suelen ordenar. La forma usual de hacerlo
es realizando un recuento y posteriormente formar una tabla con distintas columnas.
Primera columna, xi
Está formada por los distintos valores que puede tomar la variable estadística (ordenados de menor a
mayor si se trata de una variable cuantitativa). Si la variable a estudio es cuantitativa continua, o discreta pero con
muchos valores distintos, los datos deben agruparse en clases o intervalos. En estos casos, esta primera columna
se divide en dos, una para los intervalos y otra para la marca de clase, que es el valor medio de cada intervalo y se
calcula como la semisuma de los extremos del intervalo.
Para construir los intervalos hay que tener en cuenta:
- Se localizan los valores extremos a y b y se halla su diferencia (recorrido) r = b - a
- Se decide el número de intervalos que se quiere formar, teniendo en cuenta la cantidad de datos que
se poseen. Es conveniente que el número de intervalos esté entre 6 y 15. - Se busca un número entero un poco mayor que el recorrido y que sea múltiplo del número de
intervalos, r ' . - Se forman los intervalos, de modo que el extremo inferior del primero sea algo menor que a y el
extremo superior del último sea algo mayor que b. Es deseable que los extremos de los intervalos no
coincidan con ninguno de los datos, pero si esto ocurriera, se forman los intervalos teniendo presente que
el límite inferior de una clase pertenece al intervalo, pero el límite superior no pertenece intervalo, se cuenta
en el siguiente intervalo.
Segunda columna, fi
Se sitúan en ella las frecuencias absolutas: fi, que es el número total de veces que aparece el valor xi
de la variable estadística, o el número de valores de la variable que hay en un determinado intervalo.
La suma de todas las frecuencias absolutas es el tamaño de la muestra o población a estudio (N), es decir:

Tercera Columna, Fi
En ella se colocan las frecuencias absolutas acumuladas: Fi que son las sumas de todas las frecuencias
absolutas correspondientes a los valores anteriores a xi y la suya propia.
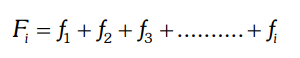
Cuarta columna, hi
La colocamos cuando nos interesa saber cuál es la proporción del número de individuos con un valor
determinado respecto al total. Para ello calculamos la frecuencia relativa o proporción: hi que es el cociente que
resulta de dividir su frecuencia absoluta (fi) entre el número total, N, de individuos.
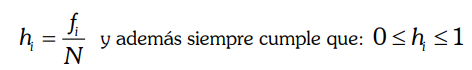
La suma de todas las frecuencias relativas es la unidad.
Quinta columna, Hi
En ella se colocan las frecuencias relativas acumuladas: Hi que son las sumas de todas las frecuencias
relativas correspondientes a los valores anteriores a xi y la suya propia.
![]()
Sexta columna, pi
Se calculan los porcentajes, que es el tanto por ciento que representa el valor xi respecto del total. Se
calcula multiplicando la frecuencia relativa hi por 100 (o mediante una regla de tres)
![]()
La suma de todos los porcentajes es 100.
Séptima columna,Dx
En ella escribiremos la diferencia en valor absoluto entre la medida xi y la media, que luego nos servirá
para calcular la desviación media.
![]()
Si se trata de una tabla de datos agrupados en intervalos, entonces en esta columna aparecería:
![]()
Además de estas 7 columnas vamos a utilizar otras dos, que nos vendrán muy bien para calcular algunos de los
parámetros estadísticos. Estas columnas van a ser, la columna octava, en la que aparecerá el producto xi·fi y la columna novena en la que aparece el producto xi2·fi
Con todo esto, nuestra tabla de recogida y análisis de datos sería de la forma:
